BioGeometry
Start of topic | Skip to actions
We say that a graph G satisfies a Laman condition for 3d if every induced subgraph (V,E) with |V|>2 satisfies 3|V|-6 >= |E|.
Jacobs claimed that a graph was rigid in 3d if it satisfied a Laman condition and had no implied hinge. He defined implied hinges in terms of rigid components of the graph (maximal sets of vertices that have no relative motion other than the distance-preserving Euclidean motions). His proof was based on what is essentially an assumption (an observation from a thought experiment in his paper) that: "Implied constraints acting on a rigid cluster within a network can only be imposed by connecting rigid clusters through implied-hinge joints."
We would like to give a combinatorial definition definition of implied hinges. The easiest would be to say that G has an implied hinge {a,b} if there a subgraph (V,E) that achieves equality, 3|V|-6 = |E|, that can be decomposed into (V1,E1), (V2,E2) with
Non Thm For a graph that has no implied hinges and satisfies a Laman condition for 3d, generic embeddings in 3d are rigid.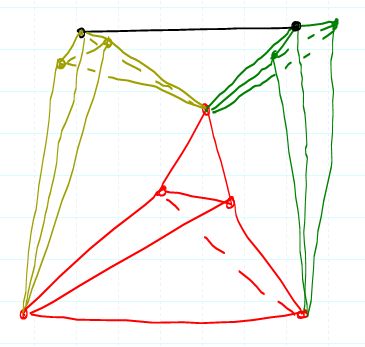 First, two properties of implied hinges:
First, two properties of implied hinges:
Lemma Any graph (V,E) that satisfies two of the following conditions, also satisfies the third:
Problem case: If G-{v} becomes rigid, then we know that all edges of G-{v} are independent. An edge of v must have been redundant, because otherwise we would have created a new motion by removing v. We can try to add an edge between neighbors of v (they can't already contain a K4 because with v they would form a K5, violating Laman's condition.) but doing so might violate the Laman condition for a rigid subgraph (if it does so for a non-rigid subgraph, then this subgraph is a smaller counterexample). If a single subgraph contains four neighbors of v, then adding v back shows that G violated a 3d Laman condition. Thus, any subgraph contains 2 or 3 neighbors of G. If a subgraph contains 2, then it must be the only one or we have an implied hinge. If a subgraph contains 3, then v is determined rigidly by the subgraph, and it is the 4th edge that is redundant.
If adding (p,q) forms an implied hinge V1,V2\subset V-{v}: we assume (wlog) that adding edge (p,q) to the subgraph for V1 increases its edge count to 3|V1|-6=|E1|, whereas V2 already had the full count. (Note that this implied hinge did not exist before adding (p,q), so both vertices p,q must lie in one of the hinge sets.) Let {a,b} = V1\cap V2 denote the hinge vertices. Consider adding the edge (a,b) to the subgraph induced by V1 instead. This has the correct count for V1; it cannot violate the Laman condition for any subgraph S, because if it did then S,V2 would have formed an implied hinge in G. It can cause the creation of an implied hinge W1,W2\subset V1: we assume (wlog) that adding edge (a,b) to the subgraph for W1 increases its edge count (i.e., it containse both vertices a,b) whereas W2 already had the full count. Note that W2 and V2 are rigid subgraphs, since they are smaller than G, have no implied hinges, and satisfy the Laman condition. Each of W2 and V2 have a one degree of freedom hinge motion with respect to W1. The induced graph on W2\cup W1\cup V2 has one edge too few, so we add one edge joining non-hinge vertices v\in V2 and w\in W2. This gives us a subgraph of G that satisfies the Laman count, and has a motion. Adding (v,w) may create implied hinges, but we delete the components of those that do not contain v,w without disturbing the counts or eliminating the one dof motion that we found. What remains is a smaller counterexample, which is a contradiction.
Missing yet -- the extension of this to degree 5, where we must add 2 edges.
Thus, there is no counterexample, and every graph that satisfies a Laman condition and has no implied hinge is rigid. What remains to show is that graphs that satisfy a Laman condition and have an implied hinge are not rigid. For this we can use the rigidity matrix, and show that some constraint is redundant. To be filled in. -- JackSnoeyink - 20 Jun 2005
to top
- |V1|,|V2|>2,
- V1\cup V2 = V
- V1\cap V2 = {a,b}
- E1\cup E2 = E
- E1\cap E2 = \emptyset,
Non Thm For a graph that has no implied hinges and satisfies a Laman condition for 3d, generic embeddings in 3d are rigid.
 First, two properties of implied hinges:
First, two properties of implied hinges:
- In a graph G with a implied hinge, the only edges between vertices hinge are in E1\subset V1xV1 and E2\subset V2xV2. In particular, G does not contain any edge from (V1-{a,b})x(V2-{a,b}). It also lacks the edge (a,b). These claims follow from the 3|V|-6=|E| counts for these subgraphs.
- If G has no implied hinge, then no induced subgraph H of G has an implied hinge. (The contrapositive, if H has in implied hinge then G has an implied hinge, follows immediately from the definition.)
Lemma Any graph (V,E) that satisfies two of the following conditions, also satisfies the third:
- The graph (V,E) is rigid.
- The rows of the rigidity matrix of any generic embedding of V into 3-space are independent.
- The number of edges |E|=3|V|-6.
- The reader can check exhaustively that any counterexample must have > 3 vertices.)
- Since G is minimal and has no implied hinges, if it contains a proper induced subgraph with v vertices and 3v-6 edges, then that subgraph must be rigid or we would have a smaller counter example.
- As a corollary of 2, adding an edge between two vertices in relative motion cannot cause a subgraph to violate the Laman condition.
Problem case: If G-{v} becomes rigid, then we know that all edges of G-{v} are independent. An edge of v must have been redundant, because otherwise we would have created a new motion by removing v. We can try to add an edge between neighbors of v (they can't already contain a K4 because with v they would form a K5, violating Laman's condition.) but doing so might violate the Laman condition for a rigid subgraph (if it does so for a non-rigid subgraph, then this subgraph is a smaller counterexample). If a single subgraph contains four neighbors of v, then adding v back shows that G violated a 3d Laman condition. Thus, any subgraph contains 2 or 3 neighbors of G. If a subgraph contains 2, then it must be the only one or we have an implied hinge. If a subgraph contains 3, then v is determined rigidly by the subgraph, and it is the 4th edge that is redundant.
If adding (p,q) forms an implied hinge V1,V2\subset V-{v}: we assume (wlog) that adding edge (p,q) to the subgraph for V1 increases its edge count to 3|V1|-6=|E1|, whereas V2 already had the full count. (Note that this implied hinge did not exist before adding (p,q), so both vertices p,q must lie in one of the hinge sets.) Let {a,b} = V1\cap V2 denote the hinge vertices. Consider adding the edge (a,b) to the subgraph induced by V1 instead. This has the correct count for V1; it cannot violate the Laman condition for any subgraph S, because if it did then S,V2 would have formed an implied hinge in G. It can cause the creation of an implied hinge W1,W2\subset V1: we assume (wlog) that adding edge (a,b) to the subgraph for W1 increases its edge count (i.e., it containse both vertices a,b) whereas W2 already had the full count. Note that W2 and V2 are rigid subgraphs, since they are smaller than G, have no implied hinges, and satisfy the Laman condition. Each of W2 and V2 have a one degree of freedom hinge motion with respect to W1. The induced graph on W2\cup W1\cup V2 has one edge too few, so we add one edge joining non-hinge vertices v\in V2 and w\in W2. This gives us a subgraph of G that satisfies the Laman count, and has a motion. Adding (v,w) may create implied hinges, but we delete the components of those that do not contain v,w without disturbing the counts or eliminating the one dof motion that we found. What remains is a smaller counterexample, which is a contradiction.
Missing yet -- the extension of this to degree 5, where we must add 2 edges.
Thus, there is no counterexample, and every graph that satisfies a Laman condition and has no implied hinge is rigid. What remains to show is that graphs that satisfy a Laman condition and have an implied hinge are not rigid. For this we can use the rigidity matrix, and show that some constraint is redundant. To be filled in. -- JackSnoeyink - 20 Jun 2005
- Jacobs-implhinge.pdf: D J Jacobs 1998 J. Phys. A: Math. Gen. 31 6653-6668
- rigidity.hndt.pdf: Good rigidity handout by D.R. Woodall
to top
| I | Attachment  | Action  | Size | Date | Who | Comment |
|---|---|---|---|---|---|---|
| | rigidity.hndt.pdf | manage | 115.0 K | 14 Jun 2005 - 09:42 | JackSnoeyink | Good rigidity handout by D.R. Woodall |
| | Jacobs-implhinge.pdf | manage | 168.0 K | 23 Jun 2005 - 07:46 | JackSnoeyink | D J Jacobs 1998 J. Phys. A: Math. Gen. 31 6653-6668 |
| | noimplhinge.jpg | manage | 23.2 K | 23 Jun 2005 - 08:19 | JackSnoeyink | no implied hinge |
| | slideshow.mov | manage | 346.7 K | 24 Jun 2005 - 13:47 | AndreaMantler |
Edit | Attach image or document | Printable version | Raw text | More topic actions
Revisions: | r1.7 | > | r1.6 | > | r1.5 | Total page history | Backlinks
Revisions: | r1.7 | > | r1.6 | > | r1.5 | Total page history | Backlinks