TModeling
Start of topic | Skip to actions
Interpolatory subdivision surfaces
One of the major mathematical developments in this project is Charles Chui and co-authors' work on Interpolatory SubdivisionSurfaces. The restriction that a subdivision surface should interpolate the given data (as opposed to approximating it) says that once the coordinates of a point are chosen, then it cannot be moved, which works against smoothness, and typically requires larger neighborhoods be used for subdivision stencils. Chui and co-authors have shown that if you also attach some additional information (which is related to surface normals) to each point, you can still get interpolation and smoothness from a one-ring. See Charles papers in Resources for technical details, especially this one, published in CAGD'08: We have implemented these in MATLAB to experiment with fitting (see InterpolatorySubdivisionDemo) and in tin2dem, one of our StreamingModules. -- JackSnoeyink - 02 Jun 2008 Slides from Wenjie on handling extraordinary points added. -- JackSnoeyink - 11 May 2006Old comments
We've done a lot since the initial work on interpolatory subidvision surfaces, but these old comments are still a good introduction, so I leave them.Subdivision surfaces in graphics & terrain
In graphics, a subdivision surface is an easy way to smooth a polygonal object to as much detail as you wish. 98 siggraph course notesThe elements of subdivision surfaces
Different rules give different properties of the resulting surface, but the basic idea is the same. Start with a mesh and alternate operations of refinement on the graph of the mesh, and averaging on the geometry. I'll focus on triangle meshes.Refinement
The easiest way to refine triangles is to add a new point on every edge and break each triangle into four. The figure shows a single triangle that has undergone two levels of refinement. Note that each new vertex that is not on the boundary has degree 6; such points are called regular and non-degree-6 points are called extraordinary. Extraordinary points are a vanishingly small fraction of points after a few levels of refinement.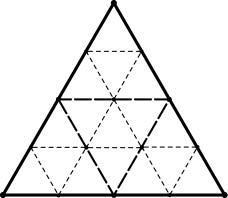
Averaging
The positions of new vertices can be computed from old in many ways. For the 1-4 division of triangles, it is common to consider two cases: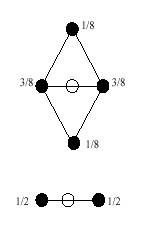
- for boundary edges, take the midpoint of the two end vertices
- for non-boundary edges, average the neighboring vertices with weights 3/8 and the other vertices in the neighboring triangles with weights 1/8, so the total weights sum to unity.
Demo
See the 3d Java demo from www.subdivision.org, which uses quadrilaterals.Use of subdivision surfaces for terrain
In this work by Ertl and co-authors, the main point of using a subdivision surface is its ability to display data at different levels of detail, including going beyond the detail present in the data. (Fractal terrain generators behave very like subdivision surfaces with funny averaging rules.) * subdivterrainrendering.pdf: Ertl et al. use subdivision for terrain rendering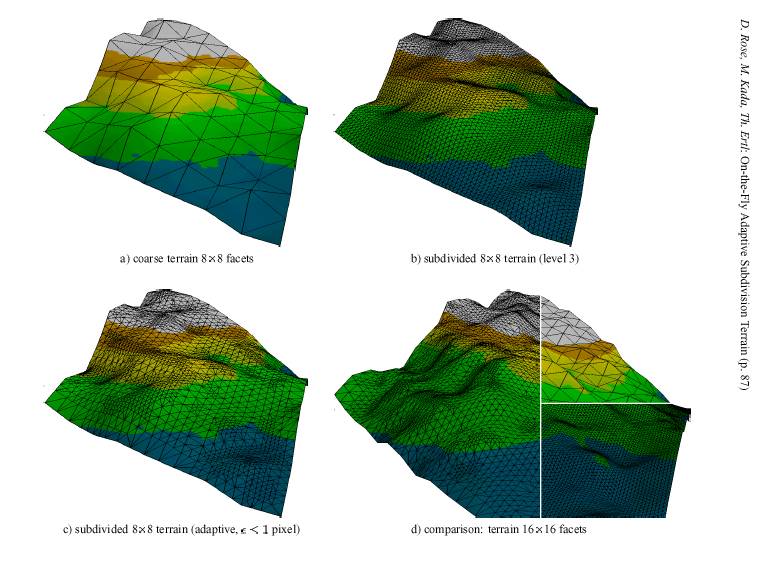
The 4-8 subdivision
- 48.pdf: Velho & Zorin on 4-8 subdivision, using mathematical notation like that of Chui.
- Hierarchical, piecewise linear versions of this subdivision have been used in LOD terrian rendering such as SOAR
 and TopoVista
and TopoVista
Mathematics of subdivision surfaces
As with any surface representation, we would like subdivision surfaces to satisfy expressibility and smoothness properties, such as being able to reproduce low dimensional polynomials from sample points and avoiding spurious ripples or oscilations. Since the surface is specified procedurally, we need to write it mathematically to do analysis.A recurrence
The subdivision surface is the limit of the refinement and averaging procedure. To analyze surface properties, and how they depend on the parameters chosen, wavelet and spline folks capture the refinement and averaging by a single recurrence formula: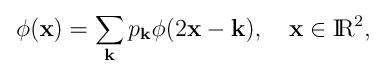
You can interpret this as follows: By simplifying the geometry to a lattice, which effectively captures behaviour at regular points, we can write the refinement as just a scaling of the lattice (2x) and invariance under translation to lattice points (-k). The averaging is captured by weights (p_k) that sum to unity and are non-zero at the few neighboring lattice points that contribute to the averaging scheme. In more detail:
- The subdivision surface phi(x) satisfies a recurrence relation:
- If you consider a lattice in the plane, and sum over all points k in the lattice,
- and if you imagine scaling the plane (2x), or equivalently halving the lattice, then you'll see that lattice points appear at all the old points and at midpoints of every edge,
- and if you translate the basis function to each lattice point (-k),
- and then average the contributions with a weight (p_k) dependent on each lattice point k that you translated to,
- then you reproduce the function phi(x).
CK's smooth interpolation from a single ring
There main freedom in the recurrence formula is the choice of averaging parameters. If we want symmetry and reproducability of constants, then the only way to get more freedom is to take more lattice points -- larger stencils, with more special cases due to possible arrangements of extraordinary points. CK Chui (working with Qingtang Jiang) propose to give more control with smaller stencils by generalizing the formula to matrix weights The idea is that along with the xyz coordinates of the vertices can be some additional (hidden?) coordinates that control smoothness, etc. These coordinate values are mixed in with the Cartesian coordinates by the matrix weights, but are otherwise ignored when calculating the surface.
It seems that even the subdivision rules for the 1-4 triangle split can be reduced to edge rules if one uses matrix weights for the different directions of edges.
The idea is that along with the xyz coordinates of the vertices can be some additional (hidden?) coordinates that control smoothness, etc. These coordinate values are mixed in with the Cartesian coordinates by the matrix weights, but are otherwise ignored when calculating the surface.
It seems that even the subdivision rules for the 1-4 triangle split can be reduced to edge rules if one uses matrix weights for the different directions of edges.
 Charles says that using matrix weights can give subdivision refinement rules that use a single ring neighborhood, yet have specified smoothness.
Charles says that using matrix weights can give subdivision refinement rules that use a single ring neighborhood, yet have specified smoothness.
- Refer to 18ff in DARPA_GEO_Nov4_05.ppt: Wenjie & Charles' slides from progress meeting
- CJsubd1.pdf: Chui and Jiang Paper on subdivision refinement with matrix weights; the last couple of subsections do 4-8 subdivision with simpler averaging rules.
- Interp_I.pdf: Main paper on matrix weights for subdivision surfaces
- extra_vertex.pdf: Handling extraordinaray vertices in subdivison surface with matrix weights
Suitability for terrain models
As I see it, there are some "research opportunities" before this scheme can be effectively used for terrain models.Subdivision informed by detail data
In graphics, subidivsion surfaces are used to make coarse control polygons generate smooth surfaces. All of the information for the surface is contained in the control polygon and the choice of stencils and weights for the refinement and averaging procedures. In terrain models, we would like to send a small amount of information in a coarse model and refine by adding details where needed -- information should be distributed through the refinement so that it need not all be sent up front. Thus, the refinement should be driven by user interest and the "averaging" should be informed by detailed data.Find a wavelet basis for errors
To address the previous, we want to capture the error for a surface from its subdivision approximation. The ideal would be to capture this with an orthogonal (or semi-orthogonal) basis of wavelets.- What are our chances of capturing error with a wavelet basis?
- Should we use an averaging subdivision instead of interpolating to keep wavelet coefficients small?
- pre04-02.pdf: Wu and Liu: orthogonal and semi-orthogonal wavelets (called wavelets & prewavelets) viewed in the lattice based refinement formula
How do we choose the hidden information?
I don't know how to choose the hidden coordinates at a vertex -- might we be able to use them to tune surfaces to the task we have? E.g., water under the influence of gravity forms most terrain: Can we tune subdivision surfaces to have sharper ridges and smoother valleys and to avoid local minima in areas where water flows?Work out special cases for extraordinary points
This is perhaps the easiest, but needs to be done to create a prototype implementation. -- JackSnoeyink - 15 Nov 2005Charles Chui replies:
Thanks for your interest. Qingtang and I are actually very happy with our results, in that we can now handle C^2 interpolation with one-ring subdivision templates as well as extraordinary vertices (for all valences) with guaranteed bounded curvature (paper under preparation). _____________________________________________________________ > >> > I'd be glad of any comments, especially on the following questions,
> > which are a restatement of questions from the end of that page:
> >
> > As I see it, you are storing hidden information with the vector valued
> > refinement function that gets brought to the cartesian coordinates by
> > averaging with matrix weights. How do you initialize this hidden information?
______________________________________________________ That (hidden information) may be another way to view our shape-contol parameters. As I mentioned to you and Wenjie after my presentation, we need to study the (surface) geometry of the subdivision surface as governed by the functionality of the shape-control parameters. This is an important topic for further investigation. I would like to use information of the neighboring terrain data to determine the initial (vector) values of the control-parameters. These values will be adjusted by the editing feature provided by the wavelet coefficients (see below). ______________________________________________________ > >
> > For terrain models, we'd like to bring in detail information as we do
> > hierarchical refinement based on level of interest in different areas --
> > how do we add this into the subdivision scheme in an elegant way?
_________________________________________________________ Ah, this was exactly my point, and I called it a "bottom-up" approach: by constructing analysis wavelets that have the multiresolution editing feature, as in my presentation. Wenjie, Qingtang, and I are working on this problem right now. _________________________________________________________ > >
> > The most elegant would be to capture the error as
> > wavelet coefficients -- is that possible?
_______________________________________________________ Definitely. There is no doubt in my mind that it can be done. Hopefully by the time we meet at Stanford next January, we can tell you more about it. ________________________________________________________ > >
> > Can the shape control be used to make the surface respect terrain
> > properties that are caused by water erosion? (e.g. far more local
> > maxima than local minima...)
___________________________________________________________ This is perhaps the most difficult problem, but I do believe it can be done. Again, as I wrote above, it depends on the geometry that could be governed by the shape-control parameters. Comments: I would like to emphasize that our approach is somewhat different from the usual surface subdivision approach, in that we must interpolate (not approximate) the terrain data. As I mentioned in the presentation, current interpolatory subdivision schemes (with scalar weights) have limitations to meet our need, and I believe that these limitations cannot be overcome without introducing matrix weights. I would also like to think of our bottom-up approach as a meshless wavelet method, since this scheme is independent of the choice of the triangulations of the terrain data. Of course it could be argued that subdivision depends on mesh in the parametric domain. Having said that, we still need an efficient triangulation scheme that gives us mainly regular vertices (of valence = 6). Do you know of such schemes in the literature? If not, do you think your team can take the lead to develop such an algorithm for scattered data? Thanks. -- JackSnoeyink - 17 Nov 2005
to top
| I | Attachment   | Action | Size | Date | Who | Comment |
|---|---|---|---|---|---|---|
| | subdivterrainrendering.pdf | manage | 367.8 K | 15 Nov 2005 - 15:51 | JackSnoeyink | Subdivision for terrain rendering |
| | subdivrules.jpg | manage | 4.1 K | 15 Nov 2005 - 19:34 | JackSnoeyink | |
| | soar.gif | manage | 1016.8 K | 15 Nov 2005 - 16:12 | JackSnoeyink | SOAR |
| | pre04-02.pdf | manage | 295.2 K | 15 Nov 2005 - 15:52 | JackSnoeyink | wavelets & prewavelets viewed in the lattice based refinement formula |
| | phiformula.jpg | manage | 3.9 K | 15 Nov 2005 - 19:33 | JackSnoeyink | |
| | Interp_I.pdf | manage | 7030.2 K | 16 Nov 2005 - 14:10 | JackSnoeyink | Main paper on matrix weights for subdivision surfaces |
| | extra_vertex.pdf | manage | 597.4 K | 16 Nov 2005 - 14:03 | JackSnoeyink | Handling extraordinaray vertices in subdivison surface with matrix weights |
| | ertl2.jpg | manage | 63.0 K | 15 Nov 2005 - 19:27 | JackSnoeyink | |
| | DarpaAlgMod.ppt | manage | 463.5 K | 11 May 2006 - 14:11 | JackSnoeyink | These slides from Wenjie roughly sketch how to handle extra-ordinary points |
| | DARPA_GEO_Nov4_05.ppt | manage | 760.0 K | 15 Nov 2005 - 15:44 | JackSnoeyink | Wenjie & Charles' slides from progress meeting |
| | CJsubd1.pdf | manage | 232.3 K | 15 Nov 2005 - 15:46 | JackSnoeyink | Chui and Jiang Paper on subdivision refinement with matrix weights |
| | 48.pdf | manage | 640.7 K | 15 Nov 2005 - 15:51 | JackSnoeyink | Velho & Zorin on 4-8 subdivision |
Edit | Attach image or document | Printable version | Raw text | More topic actions
Revisions: | r1.9 | > | r1.8 | > | r1.7 | Total page history | Backlinks
Revisions: | r1.9 | > | r1.8 | > | r1.7 | Total page history | Backlinks